독립표본 t-test
2개의 집단의 평균을 비교하는 것!
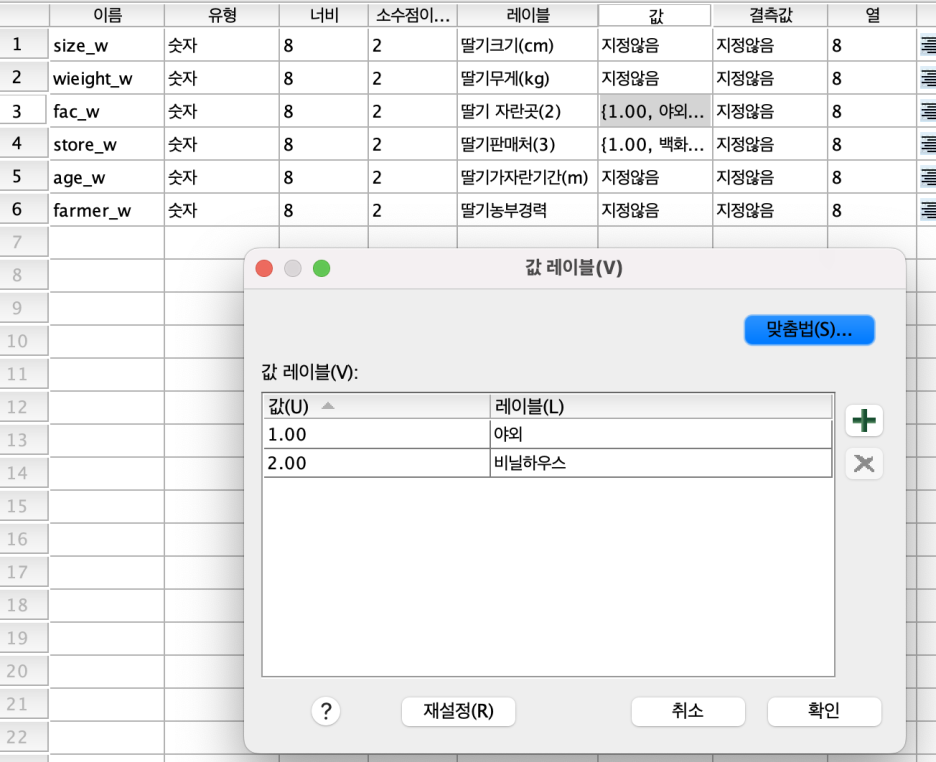
- '딸기가 자란곳'의 변수를 보면 2개의 집단으로 이루어져 있다.
- '딸기가 자란곳'에 따른 딸기 크기의 차이를 보려면?
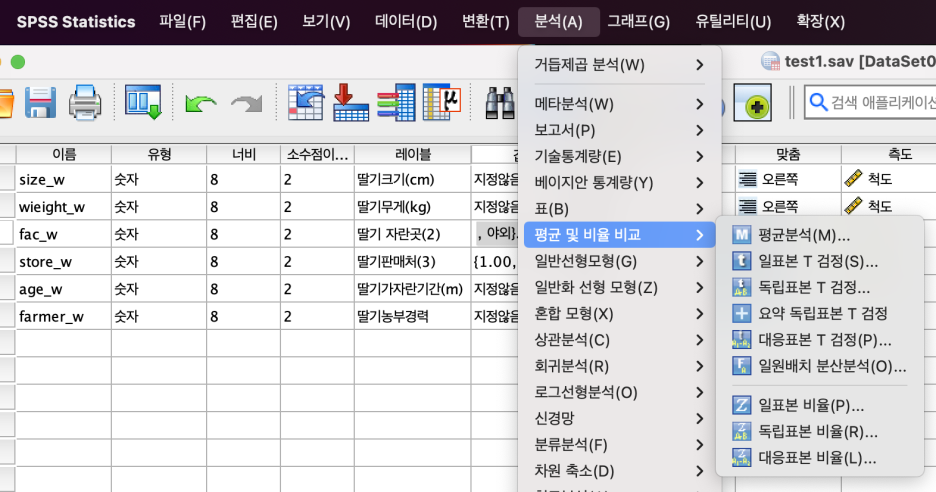
메뉴 > '분석' > '평균 및 비율 비교' > '독립표본 T 검정'
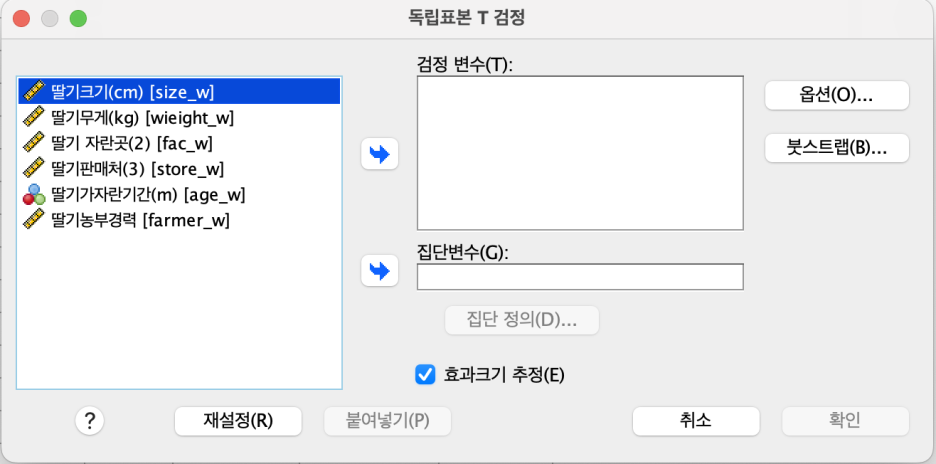
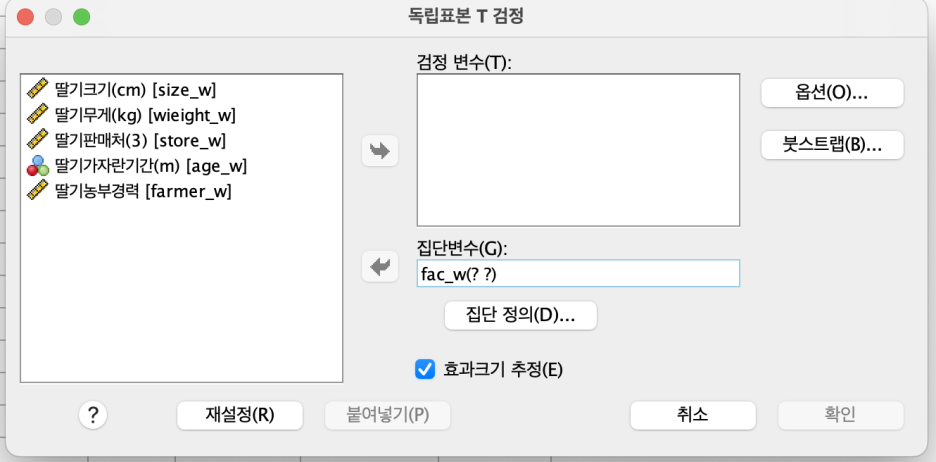
딸기가 자란 곳=집단변수
- '딸기가 자란 곳' 선택 후 '집단변수' 왼쪽 화살표 클릭 > '집단 정의'
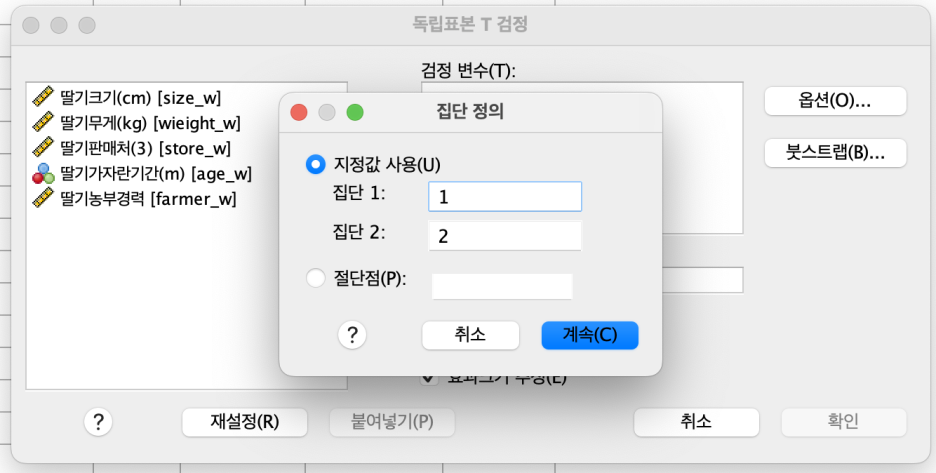
- '계속'
이번에는 '딸기크기'를 비교하자
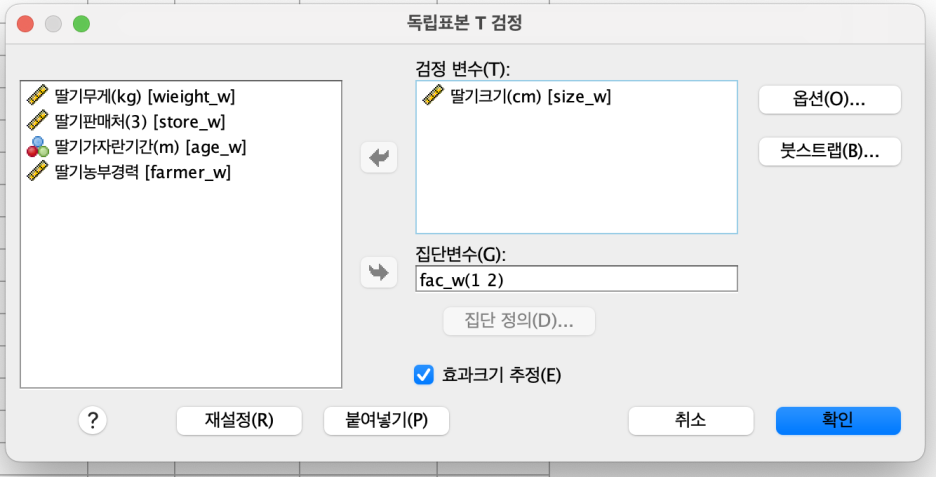
'딸기크기'를 선택 후 '검정변수' 왼쪽 화살표를 클릭 > '확인'
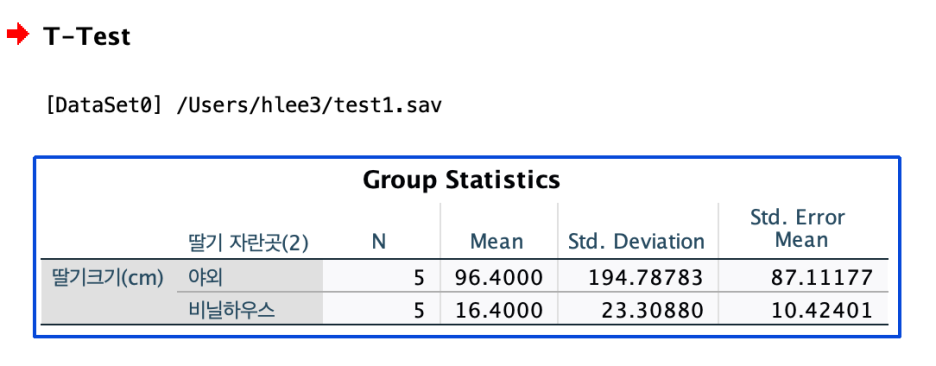
집단 통계량이 나온다.
- 야외에서 자란 딸기의 크기가 더 크다 (평균 96.4cm)
평균mean값으로 봤을 때는 크기의 차이가 있는데 과연 통계적으로도 유의한 차이가 있는가?
- 그 아래에 있는 표를 살펴보자

'독립표본검정' Independent Samples Test
- 여기서 등분산 검정(Levene's Test for Equaility of Variances)와 t-test(오른쪽)을 둘다 살펴본다.
- Levene's 의 등분산 검정에서 볼것: F값과 유의확률(Sig.)
- 유의확률(Sig.)의 값이...
- .05보다 크다: '등분산을 가정함'(Equal variances assumed)값 확인
- .05보다 작다: '등분산을 가정하지 않음'(Equal variacnes not assumed)값 확인
- .05 > .051 (작음)
- 유의확률(Sig.)의 값이...
- Levene's 의 등분산 검정에서 볼것: F값과 유의확률(Sig.)
- 이 다음부터는 t-test 결과를 살펴보자. 현재 결과는 .05보다 작으므로 여기서 윗줄 '등분산을 가정함'Equal variances assumed의 값을 보자.
- 유의확률(Significance) 양측(Two-sided p): .194
- .05보다 작다=두 집단의 평균에 차이가 있다.
- 즉, 야외에서 자란 딸기와 그렇지 않은 딸기의 크기에 유의미한 차이가 있다.
- 야외에서 자란 딸기의 크기가 더 크다=통계적으로도 유의한 차이가 있다.
- 유의확률(Significance) 양측(Two-sided p): .194
그럼 이 결과를 논문에 어떻게 쓰면 좋을까?

앞에서 살펴본 표에서
- 평균값들을 확인(+표준편차)를 논문에 써주면 된다.
- 혹은 여기에 t값과 유의확률까지 따로 적어주면 된다.(아래)

- .05보다 크다: '등분산을 가정함'(Equal variances assumed)값 확인
- 윗줄 값: t=.912 / Sig.=.388
- .05보다 작다: '등분산을 가정하지 않음'(Equal variacnes not assumed)값 확인
- 아랫줄 값: t=.912 / Sig.=.412
728x90
'하루 30분 공부 > 하루10분: 기초 논문 통계' 카테고리의 다른 글
| 6. 회귀분석을 돌리기 전 준비하기 (1) | 2022.09.22 |
|---|---|
| 5. 아노바 ANOVA (0) | 2022.09.19 |
| 3. 기초통계 SPSS 설치하고 처음 돌려보기 (0) | 2022.09.18 |
| 2. 빈도 분석, 기술 통계 분석 (2) | 2022.09.18 |
| 1. 논문 제목과 분류로 유추하는 통계 (0) | 2022.09.18 |




댓글